#1 동적 계획법 정의
분할 정복의 방법론 중 하나.
일반적인 방법은 bottom-up방식이며, 이를 재귀로 풀어 해석한게 top-down 방식이다.
1) bottom-up
점화식의 개념. 작은 단위의 해를 이용하여 점점 큰 단위의 해를 구하는 것.
점화식이기 때문에 직관적으로 이해가 되는 작은 부분은 미리 구해둔다. f(1) f(2)와 같이 앞에 2개.
네트워크 선 자르기의 문제를 통해 이해하면 다음과 같다.
문제는 길이가 n미터인 선을 1미터 또는 2미터로 자르는 경우의 수를 구해야하는 프로그램을 짜야하는 문제이다.(자르는 위치에 따라 다른 경우로 판단.)
먼저 직관적으로 풀 수 있는,
1m인 경우 f(1) = 1, 2m인 경우 f(2) = 2가지가 된다.
그리고 내가 생각하는 점화식의 규칙을 찾는 방법론이 몇가지 있는데 그 중 선택해서 고른다.
{
1번: 고정론 = 특정 경우를 고정하여서 그 전 점화식 결과를 이용한다,
2번: 규칙론 = 규칙에 따른 수식을 찾는다.
}
고정론을 사용하여 구하면 이 문제는 맨 마지막의 길이기 1로 끝난다고 고정하는 경우, 길이가 2로 끝난다고 고정하는 경우 두가지로 나누어서 점화식을 세울 수 있다.
결과적으로 점화식은
f(n) = f(n-1) + f(n-2) 가 된다.
점화식을 구하면, f(1), f(2)는 직접 하드코딩으로 대입하고, 나머지는 반복문을 통해 작은 값부터 시작해서 목표 값까지 구해주면 된다.
2) top-down
재귀 (DFS) 방법을 사용하되, 그 과정에서 이미 구한 값은 테이블에 저장해두고 사용하는 방법이다.
직관적으로 알 수 있는 이미지는 다음과 같다.
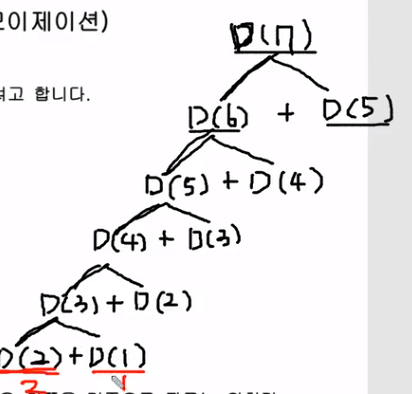
재귀로 동작하는 dfs함수 내부에, if()로 해당 인자에 대한 값이 저장되어 있다면 else문의 재귀를 수행하지 않고 바로 값을 구하는 방식으로 작동하면 된다.
결국 점화식과 같이 이전 계층과의 관계를 알아야 가능한 풀이이다. 따라서 탈출문이 두개가 된다.
DFS(int n){
//이전에 구해둔 값이면
if(dy[n] != 0){
return dy[n];
}
//점화식 조건처럼 DFS의 최하위로 내려갔으면
if(n == 1 || n == 2){
}
else{
//DFS 코드
}
}
#2 가방 문제 (knapsack 알고리즘 = 배낭 알고리즘) - 물건이 무한할 때.
독특하게, 저장하는 총량을 동적 계획법으로 기록해두는 방식이다. 이렇듯 저장하는 양을 기준으로 나누어두었기 때문에 명칭이 배낭 알고리즘인 것.
먼저 가방 수용 능력이 0그램일때도 넣어줘야 하기 때문에
(무게를 저장해두는 배열의 index) == (실제 가방의 번호)가 된다.
각 무게의 최대를 구해나가는 방식은 점화식을 세우는 방식 중 고정론과 비슷한데, N까지 담을 수 있는 무게에 3kg을 고정으로 넣었을 때, N-3의 최대값과 3무게의 Value를 더해주는 방식으로 구한다.
결과적으로 알고리즘 수행 결과는 배낭의 수용 무게마다 최적값이 들어있는 배열을 구하고, 그 배열의 마지막에 구하고자하는 최적의 가치의 값이 존재하게 된다. 아래와 같은 느낌.

하나의 최적값을 구하기 위해서 이전의 모든 구간마다 최적값을 구해야하는 알고리즘이기 때문에, 항상 효율을 추구하는 방식에 익숙해져있다면 직관성이 떨어지는 알고리즘이 될 수 있다. 따라서 더 잘 숙지해야함.
[의문?]
아무 짐(어떤 무게든 상관 없음)이나 가방에 넣는 것을 '가정'하면서 알고리즘이 시작되는데, 어떻게해서 최후에는 최적의 무게가 나올 수 있는가?
가방에 짐을 넣는 경우에 대해서 생각해보자.
경우1) 현재 집어넣는다고 가정한 짐이 최적의 짐일 경우
최적의 공간을 먼저 확보고 짐을 넣은 것이 됨.
경우2) 현재 집어넣는다고 가정한 짐이 최적의 짐이 아닐 경우
최적의 짐이 들어가게 되면 알아서 이 짐은 빠지게 됨
경우3) 현재 집어넣는다고 가정한 짐은 최적의 짐인데, 배열에 들어가는 조합의 다른 짐이 최적이 아닌 경우
경우1에서처럼 집어넣는 짐은 공간을 고정해서 넣고, 뒤에 들어올 최적의 짐이 다른 짐을 밀어내는 형태로 저장됨.
다 index 0인 앞에서부터 저장하기 때문. 어쨋든 모든 짐을 끝까지 돌기 전에는 최적의 짐이 아닌게 맞음.
생각을 반대로해보면 개인적으로 헷갈렸던 부분을 쉽게 이해할 수 있었다.
짐의 종류가 N가지인 문제에서, 임의로 짐의 종류가 N-1이라고 가정하자.
N-1을 최적의 짐 배열을 구했을 때, 마지막 종류의 N 짐을 추가했다고 생각하자.
그럼 결국 모든 최적의 짐의 조합이 바뀐다.
이 N-1을 반복하여 짐이 0개에서 1개로 늘어났을때까지 생각해보면 무슨 알고리즘인지 알 수 있다.
항상 짐이 추가될때마다 최적의 짐을 구하는 알고리즘인것.
구현 예시
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct info {
int weight;
int value;
};
int main() {
int num, maxWeight;
cin >> num >> maxWeight;
vector<info> thing;
int temp_w;
int temp_v;
for (int i = 0; i < num; i++) {
cin >> temp_w >> temp_v;
thing.push_back({ temp_w, temp_v });
}
//가방에 아무것도 담을 수 없을 때, 0도 있으므로 배열을 하나 더 선언해준다.
vector<int> knapsack(maxWeight + 1, 0);
//짐 종류만큼 반복
for (int y = 0; y < num; y++) {
for (int x = thing[y].weight; x < maxWeight+1; x++) {
knapsack[x] = max(knapsack[x], knapsack[x - thing[y].weight] + thing[y].value);
}
}
cout << knapsack[maxWeight];
return 0;
}
#3 가방 문제 : 물건이 무한하지 않을 때
효율적인 짐을 무한하게 넣을 수 없을 때 문제 풀이법이 된다.
비효율적이나 원리를 이해하기 위한 2차원 배열
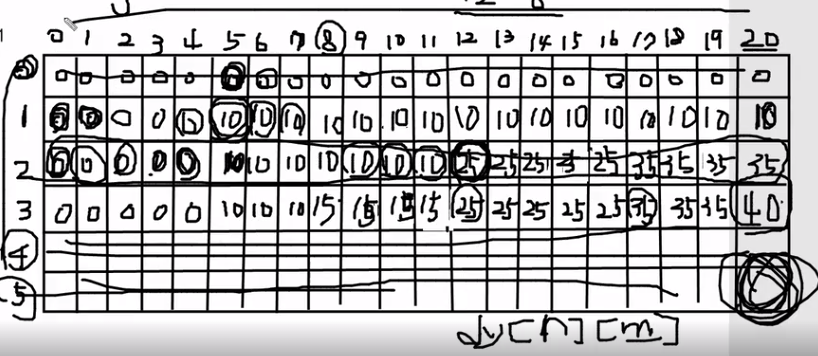
이를 일차원 배열로 만들 수 있는데, 그 원리는 결국 다음과 같다.
앞선 배열의 계산을 할 때 max(dp[n], dp[n-weight] + value[]) 를 앞에서부터 해오는 것은, dp[n-weight] 가 이미 계산하고 지나간 최고 효율의 가치이기 때문이다.
그런데 일차원으로 바꿔주면 뒤에서부터 계산한다.
(1) 앞에서부터 계산하고, (2) 앞을 참조하면서 계산하는 최고 효율의 가치는,
앞을 참조할 때, 앞에서부터 계산해왔기 때문에 최고 효율을 위해 그 물건을 이미 넣었을 수 있다.
그러나 (1) 뒤에서부터 계산하고, (2) 앞을 참조하면서 계산하는 최고 효율의 가치는
앞을 참조할 때, 이 물건을 넣었을 때의 가치가 계산되어있지 않기 때문에, 중복해서 물건을 넣지 않게 되는 것.
예시 코드는 아래와 같다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int num, maxWeight;
int weight, value;
int maxValue = 0;
cin >> num >> maxWeight;
vector<int> knapsack(maxWeight + 1, 0);
for (int i = 0; i < num; i++) {
cin >> weight >> value;
for (int y = maxWeight; y >= weight; y--) {
knapsack[y] = max(knapsack[y], knapsack[y - weight] + value);
}
}
maxValue = knapsack[maxWeight];
cout << maxValue;
return 0;
}'알고리즘 문제풀이' 카테고리의 다른 글
| 모듈러 연산 정리와 이항계수 문제 풀이 (0) | 2024.01.12 |
|---|---|
| 우선순위 큐 (Heap) 구현하기 (0) | 2024.01.08 |
| C++ 문자열 자르기 (1) | 2023.11.19 |
| 재귀 메모 (2) | 2023.11.18 |
| 자료구조 & 알고리즘 문제 풀이 개요 (0) | 2021.06.20 |





